Ein weiteres Beispiel ist die 1kg China-Wägezelle zum Testen auf meinem Schreibtisch:
Keine hardware-basierte, die in den Datenblättern manchmal drinnen steht meinst du? Ansonsten schaut das ja mit fast r = 1 sehr gut zu korreliert und softwaretechnisch könnte man die vermutlich gar nicht so schlecht kompensieren.
Ich habe die Temperaturdrift der Boschzelle H40A auf der Terrasse bei Nachtfrost untersucht:
Auch in der Vergrösserung sieht das relativ gut aus:
Sorry to come back to a topic that has already been discussed quite a lot but I would like to better understand.
I am using H40 load cells from Bosche. I have calibrated them and i apply a temperature compensation which is a simple linear function of temperature. Below is the graph of what I measure with the best load cell that I have when no load is applied to the scale. See graph below. With temperature compensation, max error is 25g and mean error is 5g (my worse load cell has error ~2.5 higher). I can probably live with that (at least with the best one) but I really don’t understand why I have so much more fluctuations during day time than during night. Initially I thought it was because the load cell was receiving direct sun light but when I make sure the scale is in the shadow, the fluctuations are the same.
Any idea ?
The wiring between the cell and the analog-to-digital-converter (ADC) changes its impedance while its temperature is changes. Try to keep the wire between those as short and as thermal shielded as possible. Looking at the graphs: Is the wire or the cell exposed to the sun during sunset, and less during sunrise?
Makes sense, thank you ! I’ll try to shorten the cables, which are indeed a bit long, partly under the sun and black… I am still puzzled by the fact the fluctuations are up and down (not only in one direction)
You don’t usually have to do that, you will even worse the situation if you ever need to extend them again (see below), even if you save the formerly removed part of the cable. You can also find designs with two 100 Ohms resistors in each wire from the strain gauge to the ADC, so it’s not about ohmic resistance.
If you can ensure the weight scale body is not exposed to sunlight which excludes simple themal expansion of the strain gauge, then you still suffer this:
That’s the key point: partly. What puzzles you, remains being the Seebeck effect.
You are observing the results of a voltage introduced by wires of different materials attached to each other and exposed to a temperature difference. This difference is created when parts of your measurement chain are exposed to different temperatures than other parts - here: e.g. electronics and scale are in shadow, whereas a (unfortunately black!) cable sees light or even sun partly during the day. By thermal conduction, this energy is propagated to the junction of the mentioned metals - and injects these voltages.
Basically it then constitutes a themocouple, that kind of sensors you would use for fast temperature measurements over a wide range. Therefore this unwanted effect is called a ‘parasitic thermocouple’ and it happens on all mounting terminals or solder spots which connect the strain gauge with your ADC. The voltages introduced here are in the same magnitude like the ones you want to measure, that is why you encounter their effect.
To compensate this, it is therefore not only important to record the actual temperature when measuring a ‘reference’ weight, but to also keep any parts from strain gauge to ADC from getting warmer or colder than others:
Remember that this unwanted voltage is not created along the wire, but only at different material on their contact spots. So reduce the number of materials involved along the chain, but most important: always strive for most uniform temperature.
I’m sure you now can explain this to yourself! :)
I repeat myself when saying that the Seebeck effect and its implications are widely underestimated. Please have a look at those various topics here which repeatedly cover these themes:
and watch how e.g. @thias, @zmaier, @Werner or @freedom2000 have solved this.
If you expose the mentioned metal contact spots to humidity, then you might create another source of voltage: an electrochemical cell… but thats another scope. It is understood to keep away humidity from electronics for various reasons.
Thanks so much to bring me up to speed with this topic. Physics is fascinating and I am happy to have met with Mister Seebeck, even if he makes my life a bit more complicated than expected !
I have been able to resolve the random fluctuations (BTW, avoiding sun on the cables was not enough, it seems the HX711 is not very stable, I had to implement some filters on the HX711 output data) but now I have another problem. As shown on the chart below it seems there is a drift over time. On the chart X axis, “00.00” mark midnight. The load cell is H40-100Kg, the assembly is pictured here below.
Any idea on what’s going on and what the problem is ?
Thanks much !
-Henri
I have asked the question in a detailed email to Bosche and here is the answer that I got from them:
Dear Henri,
thank you for your detailed description. It seems you have collected much more knowledge about load cell in beehives than we have.
Unfortunately, we cannot help with your questions. Sorry.
:-)) … seems that too much bekeepers have bothered them with too much questions and too less ordered cells!
I have seen temperature related effects with the Bosche cells but no heavy creep till now, would have expected that a heavy load over a day would perhaps lead so some creep on a new load cell but your observations last over a week. What is on the scale? I had a flower pot on a scale and have seen “nice” descending values over time. Do you have a wet wooden hive on the scale or other meterial that can dry? Any reason for real less weight?
Yes, they are probably tired with our questions. I found their answer is a nice elegant way to say that !
The weight that is on the scale is an empty hive. It is in wood and in the first days I thought it was drying because temp was increasing after a rain period. But the amplitude is too high and this is probably not the right explanation. I need to check if there is not some friction somewhere.
BTW, for those who may be experimenting the same fluctuations as those on my chart here below: I finally found what is causing the ever decreasing weight over time.
This is simply because I put an empty hive on my scale which is in bare (not painted) wood. The quantity of water in wood is actually varying quite a lot depending on ambiant humidity. I took an empty hive which was in my basement (quite humid) and it simply dried over time… Unfortunately the same can happen in real life because outside ambient humidity is varying a lot (at least in the region where I am living).
The variance of the wood moisture decreases wihtin this week displayed, as also its absolute amount slowly decreases. Can you please show another time range of the same graph, maybe one or some following weeks after the one shown?
Unfortunately, my scale is now in operation with a real hive on it. Also I believe this hive was a bit specific because it was not painted (and therefore absorbs a lot of water). All in all, humidity variation still remain an important factor I believe.
Hier auch ein entsprechender Bericht bei BEEP zum Thema »weight follows temperature«.
For documentation I add this GitHub issue were a user who adopted my scale setup did experience temperature influence and created a strategy to compensate for it:
Cheers
Hannes
FYI, I have developed a different (non linear) approach which gave me good results (with a 15mn time interval between consecutive measures, I was able to almost entirely eliminate temperature drift). The complete post on the subject with all calculation is here together with the results I obtained on real data.
Hi Clemens and others that might be interested in Seebeck T-drift compensation,
As introduced in Henri’s topic related to temperature compensation I can present a measuring method to eliminate Seebeck related temperature drift, and I think it is more appropriate to put my approach in this topic since Seebeck related drift was introduced and nicely addressed by Weef.
A few decades ago I was invited to analyze an absurd observation during the battery-charging process using a strain-gauge to measure the pressure built-up inside a battery pack by means of a Wheatstone-bridge. It appeared that the measuring set-up was corrupted in exactly the way Weef described above: for contacting the strain-gauge by 2 different metal-wires, introducing a thermocouple in series with the Wheatstone bridge output, resulting a Seebeck-effect to be mixed with the the strain gauge response. Based on the different origins of those signals, I’ve came to an approach to separate the Seebeck from the Strain-gauge signal, enabling to measure both thermal and mechanical stress of the battery during charging which finally made it into a patent.
I’m not sure if the patent has expired but recently I noticed that HBK is offering an carrier-frequency amplifier (see paragraph 2.4) to read strain-gauges (Load Cells) using the same strategy to eliminate potential Seebeck-drift as claimed by the patent.
I couldn’t find any price on the suggested HBK-amplifier but I’m quite sure it is a manyfold of the HX711 I’m using to read load-cells, for which I got encouraged to find a cheaper and simple way to enable the signal splitting strategy based on simple/cheap components and I can provide 2 tested set-ups here as an alternative to the HBK-amplifier.
So as you can read in the patent the splitting strategy is enabled by the fact that the Seebeck-effect and the Wheatstone-bridge are driven by 2 different sources. The Wheatstone-bridge signal is driven by its source voltage (provided by VAVDD of the HX711) and its respond enables to detect small variation in electrical resistance of the strain-gauges in the load-cell connected to form a Wheatstone-bridge.
On the other hand the Seebeck-effect results from a redistribution of free-electrons in a conducting material driven by the temperature-gradient over the material. This redistribution leads to small voltage gradients and is material depended. As a result 2 wires made from different materials, connected at one end, will end up with a thermo-voltage of several micro-volt per deg C temperature gradient over the 2 wires at the other end. No need to go into deeper details here as you can find more on Seebeck-effect in other publications, but the important take away is that the Seebeck-effect and Wheatstone-bridge might operate at the same voltage-level but are driven by 2 different sources: Temperature gradient (Seebeck-effect) and Source voltage (Wheatstone-bridge). And as a result they can be separated by modulation one of the sources.
I’ll present 2 tested voltage modulation methods:
Source Voltage Modulation.
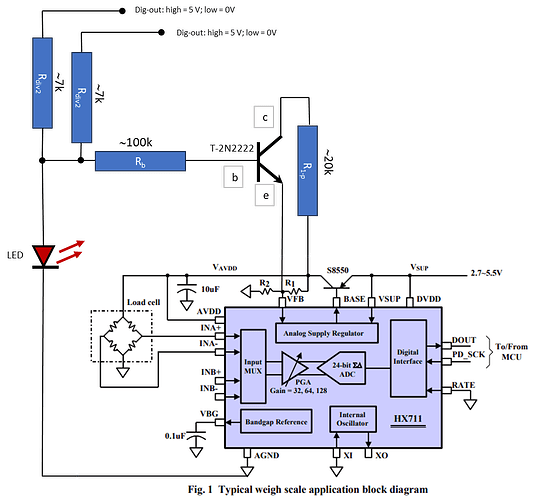
The HX711 datasheet suggests to adapt VAVDD by changing the value of R1 or R2 of the voltage divider that feeds VFB. However, for modulation purpose a software controlled adaptation of VAVDD is required and I succeeded to influence the voltage regulator by ‘injecting’ a small current into the voltage divider on the HX711, from 2 digital outputs on the Arduino UNO board by means of a transistor, a LED and some resistors connected in the circuit below.
By injecting currents at VFB (running to GND via R2) the HX711 analog supply regulator will shift VAVDD to lower values. The LED is there for signaling the modulation status but also helps to reduce noise from the Dig-out or the Arduino UNO on the realized VAVDD. The current injection circuit was build on a breadboard and connected to VFB on the HX711 by a soldered contact.
With this HX711 extension and the above Resistor settings I was able to set the Wheatstone-source voltage from the Arduino code at 4 levels: 4072, 3885, 3563 and 2475 mV by 2 digital outputs, while reading the HX711 ADC at each VAVDD level.
To interpret the response of the modulation you need to consider that the ADC on the HX711 is Ratio-metrical based, so its output-data is proportional to the ratio of the Input-voltage (A+ - A-) and the source voltage (VAVDD at E+ - E-), see table 2 in datasheet. This means for the obtained ADC output-data, the contribution of the Wheatstone-bridge will not vary with the VAVDD-setting, and for the contribution by the Seebeck-effect it will be linear proportional with 1/VAVDD. So you can separate the mixed signals by plotting the ADC-output vs 1/VAVDD.
For my 4x half bridge load cell configuration at 3 different (load) conditions this resulted in this modulation responses:
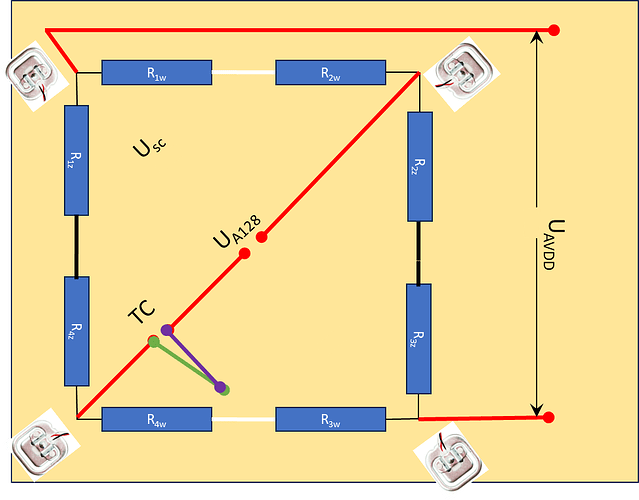
Since the graph shows only little dependency with the 1/VAVDD (VAVDD in the HX711 datasheet is the same as UAVDD for my data graphs, and Us = A+ - A-) you can conclude the ADC-response is almost free from Seebeck-effect. This might be considered good news for the quality of the set-up, but is a rather boring results to demonstrate the separating potential of the Source voltage modulation. Therefore I decided to corrupt my set-up with a [thermocouple] (Thermocouple - Wikipedia) (TC in fig below is of type K providing about 40 micro Volt per K) in series to the Wheatstone-bridge output to provide a controllable source of Seebeck-effect. The level of the Seebeck effect can be adjusted by the temperature gradient over the thermocouple.
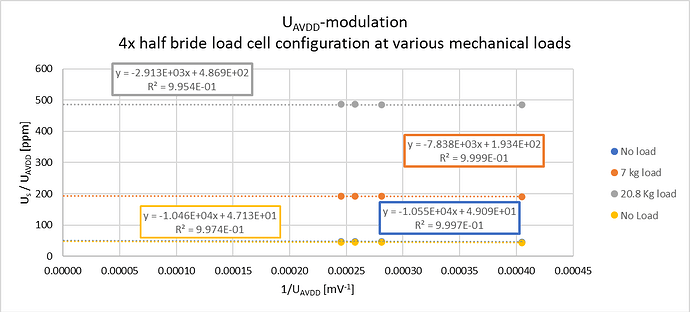
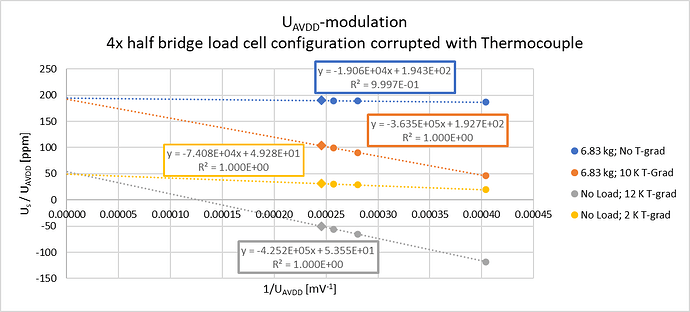
With the VAVDD-modulation for 4 different conditions (2x load combined with 4x thermal), I obtained the modulation results below:
Now the contribution of the TC Seebeck-effect is clearly demonstrated by the dependency with 1/VAVDD. Linear regression of the ADC-output vs 1/VAVDD gives:
For example the linear regression for the modulated situation with 6.83 kg mechanical load and 10 K temperature gradient over the TC, reveals an intercept of 192.7 ppm for the Wheatstone bridge load cell contribution and a slope of 3.635 E+5 nV or 0.3635 mV thermo-electrical contribution of the thermocouple (which is close to the equivalent of 10 K temperature gradient for a type K TC). Also can be seen that the, by regression obtained, intercept for the same mechanical loads are more or less the same: 194.3 ppm vs 192.7 ppm for a 6.83 kg load and 49.3 ppm vs 53.6 ppm when no mechanical load on the load cell.
These results demonstrates that VAVDD-modulation is capable in separating the Seebeck effect from the Load contribution in the HX711 ADC-response, although there might be some room for improvement since the obtained intercept values for equal loads shows some variation in the order of few ppm (equivalent of few 0.1 kg for this set-up). But without the modulation, only the diamond points in the graph would be available showing the Seebeck effect contribution was up to 100 ppm @ default VAVDD of about 4072 mV (1/VAVDD = 0.000246 mV^-1). On the other hand this might also be related to the load cell drift during the test.
Polarity modulation
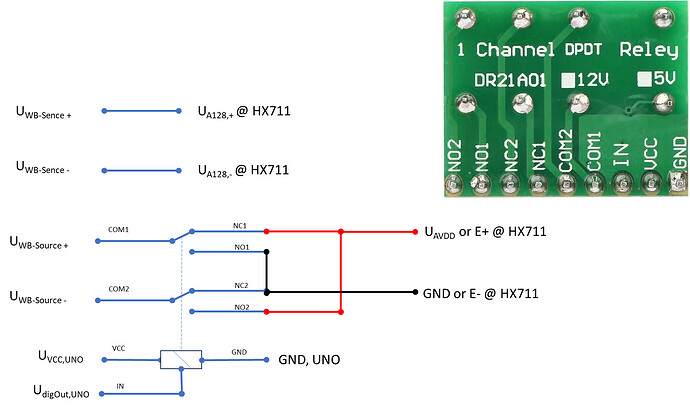
To enable the Wheatstone-bridge Source voltage polarity modulation I chose for 1 channel double polarity signal relay with Normal Open and Normal Close contacts, to be connected between the Wheatstone bridge and the HX in the figure below.
This way the polarity can be software controlled from the Arduino code by the one of the dig-outputs of the Arduino UNO, while the HX711 ADC is read for each polarity (U_A128 = A+ - A-).
Now what can we expect from the ADC-output: the contribution of the Wheatstone-bridge will flip polarity in sync with the polarity of the Source voltage VAVDD, while the contribution of the Seebeck effect remains at the same polarity independent of the Source voltage polarity. So if you subtract the ADC-output for both polarities you’ll end up with 2x the Wheatstone-bridge contribution and if you add-up the ADC-output for both polarities you’ll end up with 2x the Seebeck contribution.
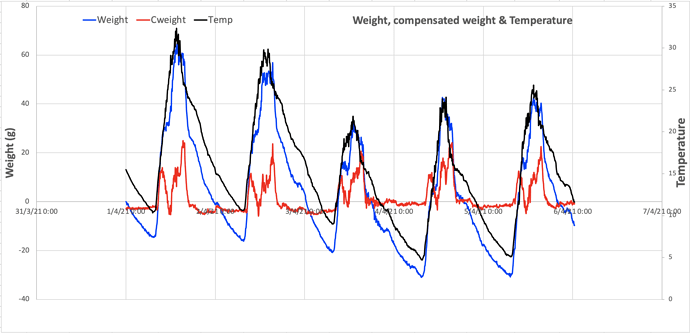
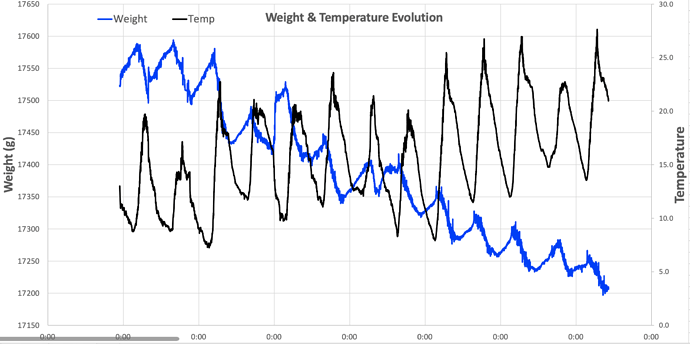
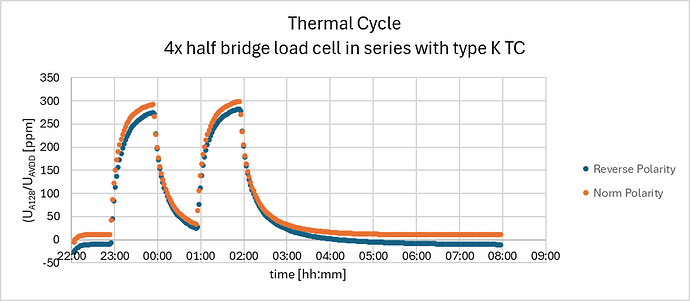
Below the recorded response of the corrupted set-up with both the load cells and the thermocouple exposed to 2x thermal cycles (heat-up to 40 deg C and cooldown to room temperature).
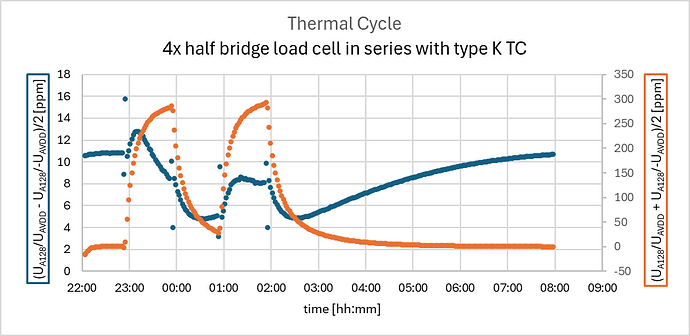
And from these you can derive the Wheatstone-bridge response (blue left y-axis) and the Seebeck-effect (orange right y-axis):
Also these results shows that polarity modulation is able the separation of the 2 composed signals with only a mild response from the Wheatstone-bridge, by the load cells, (10 ppm) on top of a huge Seebeck-effect response, up to 300 ppm. The response of the Wheatstone-bridge/load cells is without mechanical load but shows some thermal drift which is in good agreement with the response recorded without the thermocouple, and seems to be induced by a combination/interaction of thermal- en dehydration-load on the load cells during the thermal cycle.
Resume
With this I think to have shown that:
modulation is a powerful method to be able to separate signals of different sources.
these are simple alternatives to the HBK-amplifier accessible for any ambitious DIY.
Comparing both modulation methods
Source voltage modulation seems a bit more invasive to the HX711-board and requires effort to determination of the VAVDD-levels by (regular) calibration to exclude VAVDD-drift over time. Furthermore, since the Intercept is quite outside the available 1/VAVDD-range the regression error is quite sensitive to 1/VAVDD-noise or drift.
The polarity modulation can be simplified further by flipping the load cell leads connected at the E+ and E- connectors on your HX711, for which you don’t need a signal-relay or reprogramming your Arduino Code. In this way you can check at least if your set-up suffers from Seebeck effect. Note this is not the same as flipping the load cell sense leads attached the A+ an A- connectors at the HX711, as here you will also flip the polarity of the Seebeck-effect and as a result you are not able to separate both signals. If you want to go for an automated set-up, I suggest to use specific signal-relay as they are superior wrt noise.
For both methods the modulation frequency should be fast enough wrt the Seebeck-drift and load variation you like to detect. In the above same a logging-time interval in the order 1 - 2 min is used.
As you can see the voltage (Amplitude or polarity) modulation method is only able to separate electrical signals driven by different sources like Seebeck and electro-chemical, from the Wheatstone-bridge signal, but not thermal influence on the load cell’s strain gauges.
So you need to consider if you want to invest (equipment and time) in the above methods or follow the good design rules to limit the Seebeck effect as also mentioned by Weef:
Use as less as possible contacts/extension leads.
Use only (extension) leads of same material.
Limit the temperature gradient over the leads or at least try to keep the connections at the same temperature, and design the contact-point as close to each other to limit the temperature gradient.
Actually, most likely you won’t be able to exclude Seebeck sources in a circuit containing Load Cells as its strain gauges probably contain Constantan or other exotic metals-alloys (see Strain gauge - Wikipedia) for limiting temperature drift/sensitivity. Fortunately the strain gauges are attached to a metal body (most likely Aluminum) which homogenizes temperature fluctuation and minimizes the resulting Seebeck-effect.
Work in progress
The modulation has shown to be able to filter out one signal-source from a composed response. Since we are only interested on the load contribution in the HX711 ADC response, I would like to introduce load-modulation, to eliminate all response contributions related to any kind of drift. To do so I need to be able successively placing and removing the load, of the object we want to weigh, on the load cell. Given the results above I’m convinced this will substantial reduce all observed load cell drifts like Seebeck and all others. This idea is not new as I think this is also done intuitively by any one using a scale which has a tara-feature. I think this is also, in some way, integrated in professional/industrial scales, which runs in the background.
However, I’ve not jet come to a simple set-up which enables sw-controlled load-modulation. I’m looking for a suitable actuator and a mechanical-design able to lift 100 kg load to meet this application. For sure what will be unattractive is the power consumption of this feature (1 J per lift-cycle of lifting 100 kg 1 mm.) and the question I can’t answer: do the bee’s like to be rocked once in while…
Anny suggestions or help is welcome.
