Is your experiment-data by chance collected on Hiveeye’s swarm-server? If so, I would probably be tempted to try how one could apply the integration you suggest successfully afterwards, just on the raw data.
No, I have my own server, the data aren’t on Hiveeyes server. I haven’t yet implemented the algorithm in the code (will do soon…). For the test, the raw data were processed off-line.
Hi Henri / @hsors, the compensated “line” is awesome, nearly no peaks, even in a conservative view +/- 10 g mostely generated by a single spike! I played arround with some basic linear compensation formulars and got never that accuracy!
I assume that this compensation is a treatment for every single load cell with individual parameters and so variables in the formula. We have seen different “reactions” to temperature even on load cells from the same manufacturer and the same model.
Would it be a good idea to have a “average” compensation formula lets say for the Bosche H30 load cell as a result of testing e.g. five H30 cells and average the outcome or is this not a good idea because the formula is very specific for the behavior of a single cell and we would make more noise in case we treat all H30 cells with this treatment?
Would be really great try to implement this as Grafana formula in a dashboard! I asked some beekeeper from the documenta project to leave the scales empty or with a constant weight perhaps we can find some raw data at Grafana (use the drop down to inspect hive-01, hive-02, ...)
Hi Clemens !
I also have tried before different linear models with little success…
Would it be a good idea to have a “average” compensation formula lets say for the Bosche H30
Unfortunately, the parameters greatly vary by load cell. I have one LC that drifts by 1g/°C and another one by 7g/°C. Difficult to avoid an individual calibration…
Would be really great try to implement this as Grafana formula in a dashboard
I was thinking of implementing this in the scale itself (not done yet…) but if it’s possible to do that in Grafana, that is a good option. I am new to Grafana and haven’t dug into it very much; until now I was using Google Sheet with an API from a python program retrieving the hive data and loading those data into a google sheet file. I am now switching to node-red/InfluxDB/Grafana.
May you attach the raw data of your plot above in any format to this thread, I can try to import this data in Grafana (we have a bulk import option there) and we can try to implement the compensation by software. I think we need the help of Wetter / @wtf as our Grafana DJ in residence but it could be a good starting point. Manipulating the data on the visualization level has some pros but also cons, but for playing with an algorithm it may be a better option than hard coding it in Arduino code or write compensated data to database directly.
Sure, here is the file in XL format.
If it’s not clear we can set-up a call for explanation.
TemperatureCompensationLC5-vf.xlsx (246,0 Ko)
And finally, here is the code along with some explanation. I implemented it in the microcontroller and it has been running for 24H outside (external temperature ranging from +15°C to +25°C) with a 2066g mass on it; weight readout has remained stable, at +/-2g (2064 to 2068g), knowing that 2g is the resolution of my scale.
weightCompensation.cpp (2,0 Ko)
additional scale-parameters.h (1,6 Ko)
Code explanation is in the following file:
Implementation.docx (25,5 Ko)
Implementation.pdf (79.8 KB) (same in PDF format)
Dear Henri,
thank you so much for sharing the outcome of your work. After reading the accompanying document, I would like to humbly ask if you can also add the referenced file scale-parameters.h to your original post? It looks like it might be missing there.
With kind regards,
Andreas.
Sure. Here is the file. I am available for oral explanation if needed but I need to confess that I am not a good coder at all… I learnt electronics (not computing) and it was 40 years ago… I was new to C++ until a few months ago.
scale-parameters.h (1,6 Ko)
Best regards (from Grenoble/France)
-Henri
Hi Henri,
Great work, a lot of time spent and knowledge. Do you have a working code example to implement into my own code? I have been using my own scales for 4 years but the compensation has always bugged me.
Either way amazing work, well done!
Hi Adam. It should all be in the repository. Cheers.
Hi Adam ! Great to learn that somebody is looking at what I have done. I am not sure many people are interested and indeed temperature compensation is a “nice to have” feature which doesn’t exist in most commercial scales. I was actually more motivated by finding a solution to this engineering problem than by improving the weight measure precision…
Hi Henri,
I got referred to your load cell temperature compensation post on Hiveeyes, when I was exploring a post considering thermal drift management of load cells in combination with the HX711 ADC at the Arduino Forum.
In your example is shown that your approach reduced the thermal drift of a Bosch HX40 load cell by nearly a factor 8 to only 2 g (1 sigma over a 3 day period) which I think is a very good result indeed. If I understand correct the Bosch HX40 uses 4 strain gages (2 in compression and 2 in tensile mode:Single point load cell H40A | BOSCHE) in a full Wheatstone bridge and as such the load cells response is (partly) temperature compensated.
However, in your application you want to stretch the load cell into a high resolution range where its response shows some remaining temperature dependency in the order of a few g per K. Given the temperature dependency, derived by calibration, and the load cell temperature you should be able to correct for thermal variation improving the measurement resolution of the HX40. In your application you’ve measured the temperature of the environment rather than the load cell itself and you state that the load cell temperature won’t keep up instantly with environmental temperature variations because of its thermal mass and the limited heat-exchange with its environment.
To overcome this, you propose a thermal ‘model’ that estimates the load cell temperature response when it is exposed to a varying environmental temperature. A sophisticated but also elaborate approach used in various high accuracy systems where accuracy is valued above added complexity.
When I analyzed your data-file I was surprised to notice that according to your model the estimated load cell temperature is at most deviating 0.25 deg C from the ambient temperature during an ambient temperature variation of about 10 deg C per 12 hours. In your example the calculating effort to derive the load cells temperature from the ambient temperature variation with the suggested model adds up to a max correction of only 1 g compared to a more simple temperature correction using the ambient temperature.
Only if the ambient temperature variations are steeper or the delay time of the load cell is higher, the additional correction by the model will get significant with respect to your variation-goal of about 2 g. So this questions why to use the elaborate calculations which barely helps to improve the thermal drift correction, and in case it would why don’t put a temperature sensor onto the load cell directly so you obtain the load cells temperature by measurement instead of additional and elaborate calculations?
Despite this, I think, for this case, the thermal correction is quite useful and interesting as it shows to be able to reduce the measurement variation to 2 g (1 sigma over a 3 day period), and if I understand from your LOADCELL_DIVIDER value the measurement range of the H40A was 100 kg, you’ve achieved a noise level of only 20 ppm. This is at least 2-3 orders better as suggested achievable by National Instruments (How Is Temperature Affecting Your Strain Measurement Accuracy? - NI).
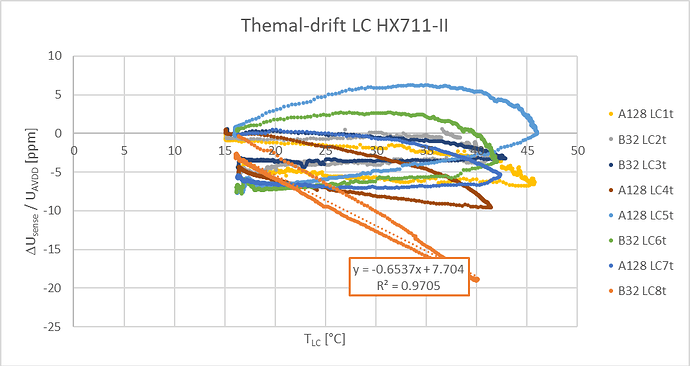
Your post inspired me in trying to extend the measurement range of some cheep halve-bridge load cells but this attempt failed due to higher drift values exceeding the thermal related drift see graph below, and for that I think the Bosch H40A load cells seem more suited.
I hope this may of be of some help for those who want to extend the normal operation range of load cells for their specific applications.
Regards,
Geert
Bonjour Geert,
I apologize because for some reasons, I didn’t get the notification about your post and therefore haven’t had a chance to respond earlier. Very sorry for that.
With my limited knowledge in physics, I believe that all what you say is perfectly correct and there is obviously room for improvement. But I also believe that this discussion is very much for “techies” like you and me but probably much less relevant for ordinary people that just want a scale which works.
I must confess that in the day to day life, temperature compensation is not a “must have” feature and cases where temperature related drift is a problem are not very usual. But it is was a nice technical topic to tackle and I enjoyed the time I spent on it as well as enjoy reading all your perfectly relevant and precise technical comments.
All the best ! Henri
PS: it good to get a confirmation that the cheap bathroom type of load scales are not suited for beehive scales.
Bonjour Henri,
Thanks for your response.
Sorry for not being clear enough, but is was not my intention to state that the thermal compensation is not required… in contrary I’m convinced that thermal compensation is of high significance to be able to push the physical limits of Loadcells as you, and ordinary people, tend to do in your application (long term stability of a few grams at a total range of 100 kg, exposed to ambient-temperature fluctuations).
And indeed it may become a too detailed technical discussion for the “non techies”, but my remark was that there are more compensation options to chose from, and, unfortunate, it requires some skills to choose wisely. I think your work is outstanding and is capable to compensate for dynamic thermal effects, which requires some skills to implement correctly.
But, as you showed in your example, it only adds stability compared to stationary, less complex, thermal compensation if the thermal dynamic effects are substantial high. I realize now that my alternative to your approach by repositioning the temperature sensor at the loadcell is also not really self explaining as it takes some insights how to mount a sensor as close as possible to, but without exposing mechanical strain to the loadcell to ensure stable loadcells readings.
All of this requires some skills to be able to implement it correctly but if you keep in mind the variety of technologies which are implemented inside an industrial-scale, that meets your requirements and achievement, are of much higher level of complexity and manifold (and thus expense) as we “techies” can imagine.
I’ve continued and partial succeeded to improve the noise/drift of the cheap/low-end loadcells but am not fully satisfied. Can you elaborate in more details on what hardware you achieved your outstanding results above, like type Bosche loadcell (including quality-grade) and accompanying data-acquisition-ADC (I’m using a HX711 green-board (cheap and brandless), which is also under suspicion for drift (my own experience but also found other posts)), and where to pursue them at acceptable expense?
Thanks in advance.
Regards, Geert
Bonjour Geert,
I am using Bosche H40 load cell and HX711 ADC for data acquisition (that I bought from SparkFun here). My results are probably a bit over optimized because during my tests the scale was in a closed box, with no direct sun shine on it. Also the load cell is only 100Kg capacity, which probably minimizes fluctuations versus 200Kg load cell.
If you happen to find a solution enabling to use the cheap bathroom scale type of load cells, that would be an incredible contribution. Keep us informed of your progress. Thanks ! Henri
I don’t think there is a solution for the bathroom scale sensors. The reason is: Not only changes in temperature are responsible for the fluctuate output but also creep, an unforeseeable and unpredictable change in weight based on different factors e.g. bathroom scale sensors are not designed for continuous load and deforming (not reversible).
But it’s OT here in this thread and we can discuss it on Scales with bathroom load sensors
Hi Clemens,
Thanks for spearing me from another feasibility-quest of cheap loadcells ;-).
However, for me they could be acceptable because I may be a strange bee in the hive and it would be fair to tell this upfront. My interest is not weighing bee’s but weighing beer, and more specific during its fermentation. During this process honey (or (grain)sugars) is converted into alcohol and carbon dioxide which leaves my ‘hive’ (fermentation-vessel) as a gas. The loss of carbon dioxide per fermentation-batch amounts in the order of 5-10% by weight and for me this an important indicator how the fermentation-process is progressing. For this I’m looking for a weighing scale that can weigh up to 100 kg with drift/variation below 0.05 (app 50 g) over a week period exposed to limited ambient variations in humidity (40 - 80) and temperature (5-10 C). From all the Hiveyees-stories I read so far I understand my requirements are peanuts to the level what hiveeyes want to achieve. So actually I’m trying to ‘steal’ some of your hiveeyes-solutions for my application. But in exchange I’m willing to share some of my insights eventually including a measuring method which will exclude Seebeck thermal-electrical parasitic disturbance in loadcell circuits. I’m not sure for bee’s but some ant-colonies do cooperate with other organisms to the benefit of both, and maybe this can work also for Hiveeyes and Brewies species. So let’s find out.
Rather to summarize than to repeat previous work I understand that you in a way were involved in a comparison of various cheap(er) single load cells activity/topic started by Juergen 6.5 years ago where you showed the Bosche H30 had the best stability performance of 20 g for a 200 kg range (0.01%)(Comparison of Different Load Cells for a 4-Point Scale). Futhermore, in this post above Henri proved to be able to reduce the variation down to only 10 g for a 200 kg range scale (0.005%) by additional temperature compensation. From other topics, concerning the loadcells stability, I understand there is no clear way yet to qualify the stability from the loadcells specification-sheet. Considering the Thermal drift and Creep specification in Juergen’s overview, I would conclude that all observed loadcell variation are more or less within spec although they may not meet your requirements. On the other hand the more expensive Bosche H30/H40 fits your requirements but I couldn’t find any specification which can confirm this. Do you have by any chance the specification-sheet for the Bosche H30/H40 wrt to Thermal drift and Creep? According to the specification I obtained for the cheap bathroom loadcells, they may perform up to at least 1 order worse, so chances of meeting your requirement are close to zero as you also concluded. I wonder if you’re requirements will bound you to expensive loadcells due to their superior performance, apart from the make you own scale joy, wouldn’t it be cheaper to pursue a balance from OpenBeeLab http://www.openhivescale.org/? Did anyone tried the physical tara-ing option, remove weigh → zero reading → replace weigh, to exclude drift effects which opens the path for cheap/inferior loadcells?
Best regards,
Geert
Hi all,
I found your post after some research about the strange behaviour of load cells.
Your analysis is very intresting.
But, I built a Scale with the economic load cells (GitHub - Slaykristian/ArniUino).
Errors are present and as you studied, there is a conclamated temperature relation.
In particular, I noted that variations depending by the action of value variation (not depending by the Celsius degrees) more that by the own final value.
I’m not an electrical engineer, but a civil engineer… But some of my colleagues that are from the first category, suggest me a solution for the error copensation.
They said that, because load cells are cheapest than yours, I can add 4 load cells with another HX711 and load these by a note weight, i.e. 2kg.
Every 30 min., when a new data read it starts, the scale reads data from the 2kg loaded group of cells, evaluate the difference due by the error, and use this parameter in order to compense the weight reading of the others 4 load cells under the hive.
What do you think about this? It could be a different solution, suitable for more cheap load cells solutions?
Thank you.
Christian
Bonjour Christian,
It’s always interesting to test new approaches but based on the randomness of the errors you get with cheap load cells, I doubt that two sets of such load cells will drift the same way. It you try, please let us know and have fun !
-Henri
