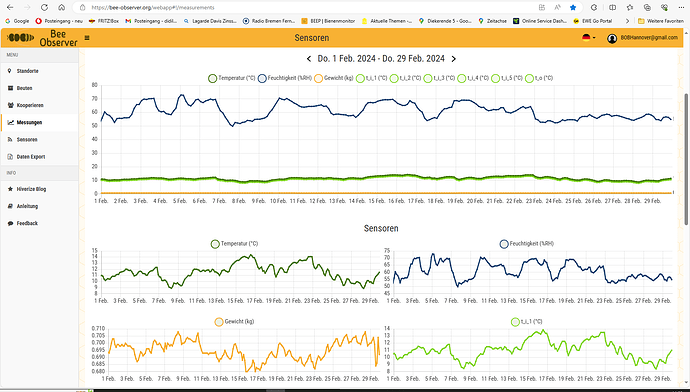
Hi Henri and others,
I’m happy to introduce a weighing procedure which compensates/reduces a manyfold of drift factors observed with cheap bathroom scale load cells, which, wrt drift-reduction, even surpasses your Temperature compensation results presented above, with the superior Bosche load cells.
As I presented above my bathroom scale load cells show complex drift patterns over time related to ambient changes in temperature, humidity or other unknown origin.
In my contribution to a topic started by Clemens related to Thermal drift, I showed that Source Voltage modulation of the Wheatstone-bridge is able to reduce for the Seebeck drift which might be incorporated in your measurement circuit design, and given the good results, I suggested to investigate the load modulations to eliminate all drift/creep components, including the Seebeck-drift.
I’ve found a way to modulate the load on the load cells and have good results with long-term stability with a standard deviation in the order of a few g over a period of half a day, while the load cells show drift levels in the order of 50 - 100 g over this period.
Load Modulation
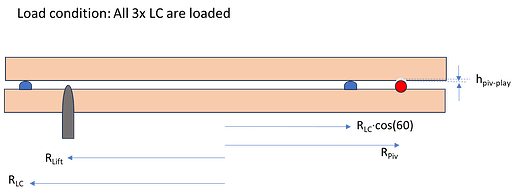
The idea is to alternately load and unload the load cells with the object to be weighed, while the HX711 is logged on both conditions.
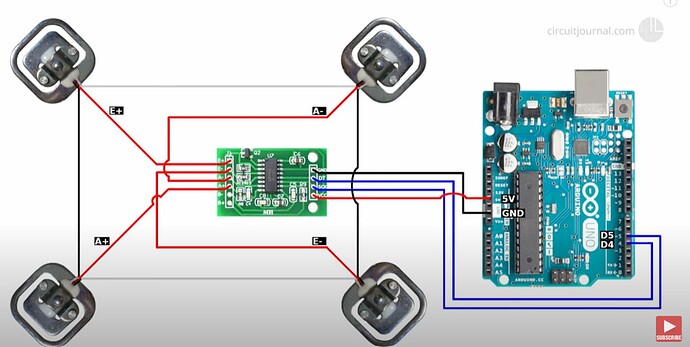
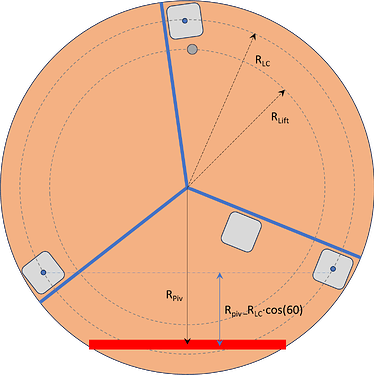
For that I’ve made a setup as sketched below.
4x cheap half bridge load cells are configured into 1 single Wheatstone-bridge. These load cells are mounted on a disk-shape base plate with 3x load cell pointing upwards and one is hanging in a pocket inside the base plate. A plateau plate is placed on top of the 3x load cells contact-points and the object to be weighed can be place on top of this plateau.
I’ve chosen for only 3 contact points:
-
Due to overdetermined mechanical conditions, 4 contact-points would lead to flatness requirements superior to my machining skills 
. As a result this would probably lead to only a situation where only 3 load cells make contact with the plateau and the chance of instable plateau wip-wapping between 2 load cells. Choosing for a 3 contact-point will give a stable contact by definition, regardless of the flatness, and by a triangular configuration this would be reasonable stable for little off center positioning of the object.
-
After individual calibration of each load cell there were only 3# load cells with comparable load-sensitivity (better 0.1 %). Since from the Wheatstone-bridge response you cannot derive how much each load cell contributes to the sum of the total weight, all load cells need to have more or less the same load-calibration, otherwise the result will largely depend on the position of the object on the plateau.
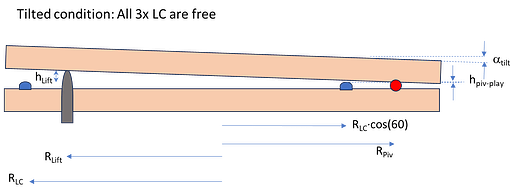
Now to enable the unloading of the load cells there is a lifting-pin (grey) which can be shift upwards by a Servo-motor. When the lifting-pin is touching the plateau the plateau will tilt to the other side un-loading the load cell which is situated to the left of the lifting-pin (see sketch). Raising the lift-pin further will tilt the plateau until it touches a red support-bar which is fixed on the base-plate, after which the 2 other load cells positioned on the right from the lifting-pin will be un-loaded.
With the right dimensional choices this can be realized by raising the lift-pin only a few mm and, since the support-bar will carry half of the plateau load, only half of the plateau-load for the Servo. Furthermore, the tilt-angle can remain under 1 deg to prevent slipping of the object from the plateau (and I think almost no disturbance for the bees to notice).
I’ve found a high torque servo (40 kg*cm about 20 Euro) which can be controlled by Arduino-code.
Load Modulation Results
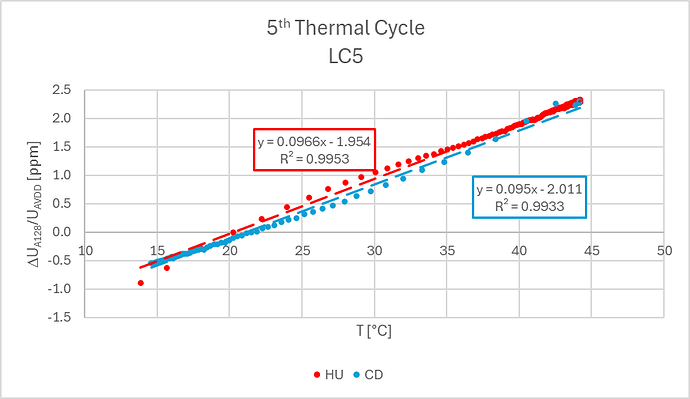
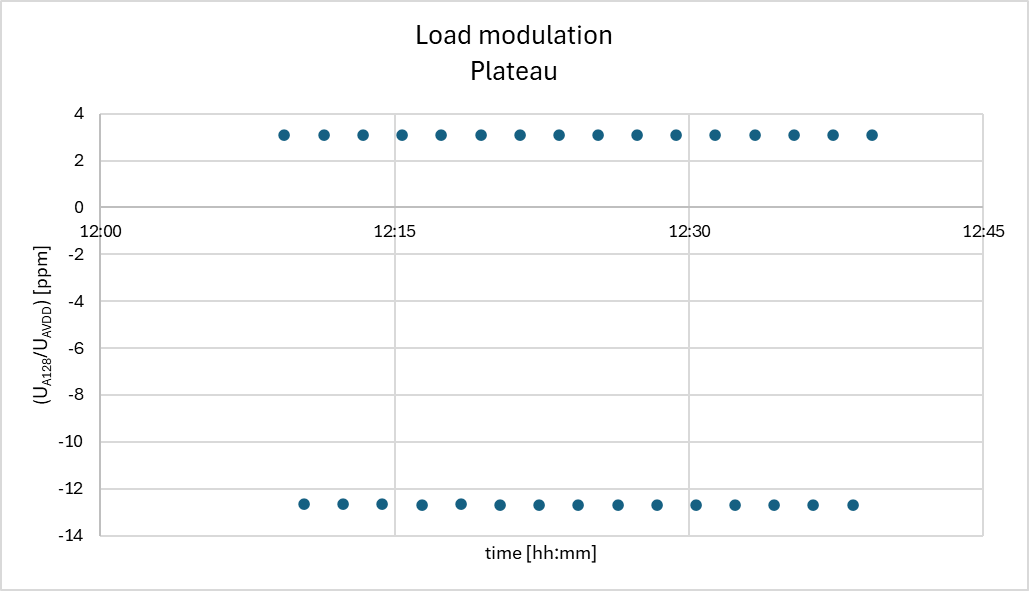
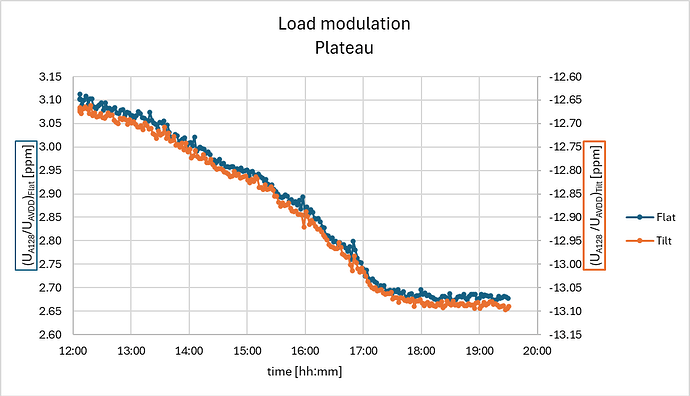
The HX711 ADC response of the Load Modulation at a frequency of 30x per hour looks like the graph below:
The upper data-points are with the load on the load cells (here only the load of the 1.46 kg plateau), and the lower data-points with the tilted plateau and thus un-loaded load cells. Zooming in in the range at both conditions for a longer period of time the drift of the load cell becomes clearly visible:
In the graph above the ADC-response of the loaded condition is given by the blue dots corresponding to the left y-axis and the orange dots for the un-loaded condition corresponding to the right y-axis, both having the same range-width. This clearly shows that over 5 h time the 4x load cell drifts over -0.4 ppm (about -40 g), but this is nearly the same for both the loaded and the un-loaded condition. Deriving the difference on ADC-response for both conditions over this period gives:
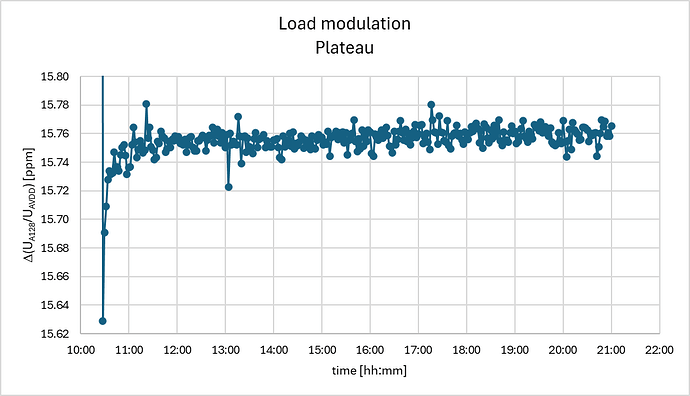
This gives a constant result with no drift but more or less random noise in the order of 0.01 ppm which is 2-3x the short-term noise I get from my ADC reading, and given the load-sensitivity of 10.8 ppm/kg this is in the order of 1 g.
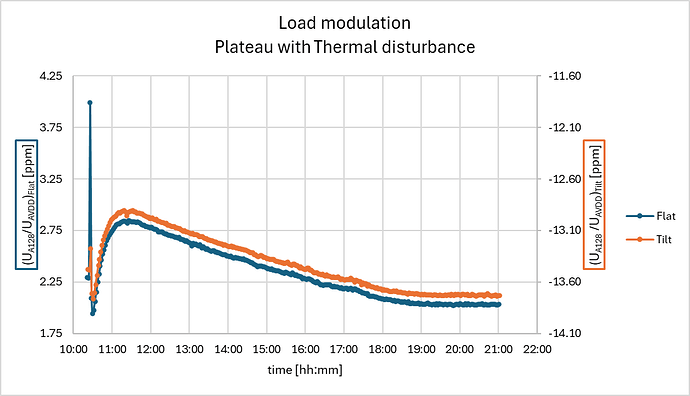
Now let’s increase the load cell drift by exposing 1 of the load cells to a hot air stream from a paint-stripper for app 1 minute:
Apart from the temperature rise this thermal-excitation also affects the hydration of the load cell which takes much longer to recover and sums up to a drift of almost +1 ppm (100 g) in the first hour, after which it takes 6 h to recover. But again the loaded and un-loaded response show the same drift and the difference appears only mildly drifting in the order of 0.05 ppm or 5 g in the first half hour and later on app 0.01 ppm (1 g) over 10 h:
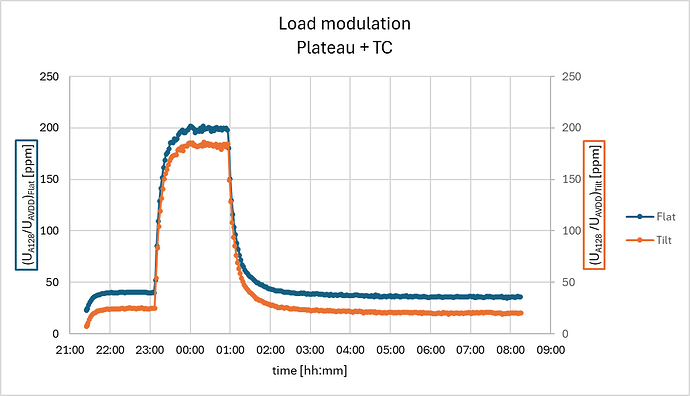
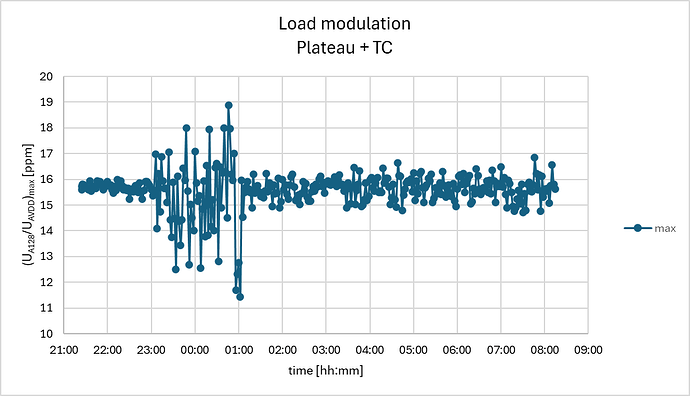
And now for the extreme case when the set-up is corrupted with a thermocouple which is exposed to a temperature cycle (load cells are exposed to ambient drift conditions):
Here the drift is 150 ppm (15 kg) in 1 hour, and again almost equal for both the loaded and un-loaded condition, resulting in the difference signal:
The drift-trend cancels out quite ok, but there is a 10x increase of more random noise (order of 10 g), partly due to noise increase on the ADC reading probably picked up by the thermocouple.
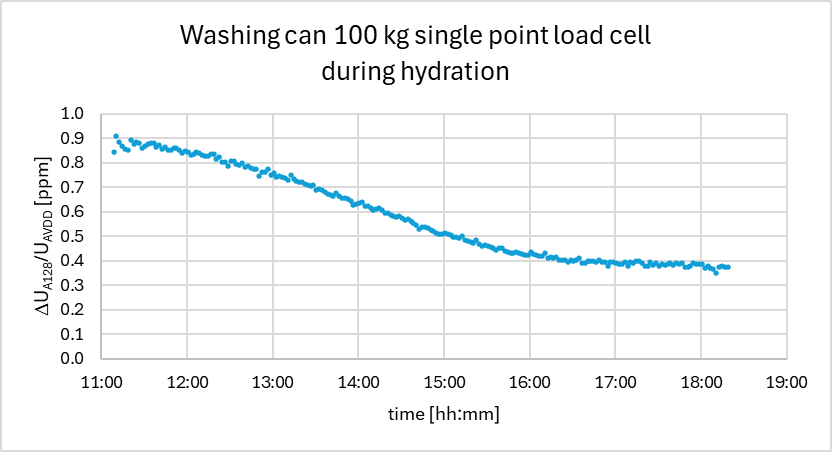
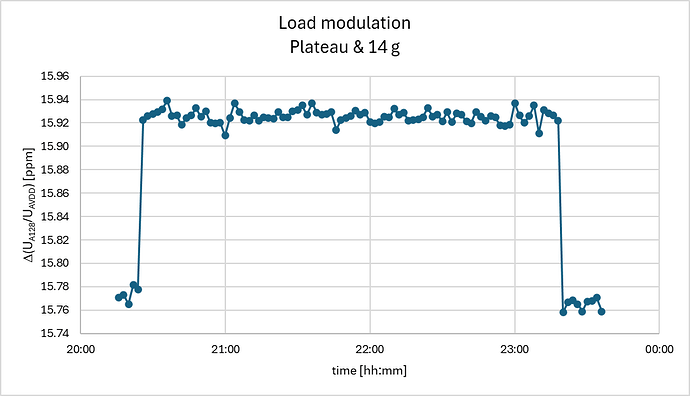
Finally I’ve placed an object of only 14 g for almost 3 h on the plateau while the load cells are drifting:
Here the drift is about -0.4 ppm/day and the placing and removal of the object is noticeable but would be exceeded by the drift in half a day. Again here the difference signal cancels the drift and reveals much clearer the load of the 14 g object:
Concluding
The above results show that load modulation has a substantial contribution in reducing the load cell drift that is affecting the weight measurement, enabling the use of cheap bath room scale load cells for high resolution hive-monitoring. Here, at best, 1 g noise at 150 kg range was realized, which is an improvement of at least 1 - 2 orders.
High loads (> 10 kg) were not tested yet, as my set-up requires some mechanical modifications to make robust load modulations possible. Never the less, I have good hope load modulation will also have high potential to compensate for the assumed creep related to deformation to a continues and high load, as the modulation frequency is sufficiently high compared to the time scale where this creep takes place, as long as the load-sensitivity remains linear and is not affected by this deformation-creep.
The lifting design needs more attention to make it sufficient robust to remain operational for long time under more extreme outdoor conditions. Furthermore, the off-grid application of load modulation will require higher battery capacity and energy source to power the tilting-servo. If all this additional effort is compensated by the load cell’s cost reduction may be questioned, for sure if you can accept some drift. However, if your application requires extra resolution, load modulation might be a valuable option.
It is not as sophisticated as Henri’s temperature compensation method but it is capable to eliminate many more drift-sources
