FFT-Implementierung / Daten der FFT-Analyse überprüfen

[clemens]

Wir sind gerade dabei die erste Software-Version [Stand 12.09.] für das Szenario

Aufnahme über I2S-Mikro > lokale FFT auf dem FiPy > Ausgabe der FFT-Daten via

cedric-cfk/fft_analyze/blob/master/fft_analyzer_with_mic.py

zu überprüfen. Dafür habe ich mit Online Tone Generator - generate pure tones of any frequency einen 400 Hz Ton erzeugt und im code START_AT_HZ = 100 gesetzt. D.h. das erste bin sollte von 100-200 Hz gehen, das zweite von 200-300 Hz usw.

result: [61.59261, 4.576358, 23.74792, 3.313573, 13.01884, 2.110722, 21.43111, 1.8991, 48.91363, 63.52398]

Damit bekommen wir schon ein lokales Maximum mit 23 bei bin 3 was ja passen würde mit 300-400 hz, aber auch 61 bei bin 1 mit 100-200 Hz und die letzten beiden bins mit 49 und 63 sind komisch.

[clemens]

Liegt es am Mikrofon?

Meine erster Überprüfung: Vielleicht liegt es gar nicht an der FFT, sondern am verwendeten INMP441 I2S-Mikrofon. Um das zu testen habe ich eine wav-Datei erzeugt, dabei den gleichem Ton abgespielt. Statt der FFT auf dem FiPy habe ich mir das Spektogramm der Audio-Datei via http://www.sonicvisualiser.org/ grafisch auf dem Rechner ausgeben lassen:

Die 400 Hz passen sehr gut, auch 600 Hz sieht man super:

Am mic scheint es also nicht zu liegen, sondern an der nachfolgenden Umrechnung und Analyse!

[clemens]

Instrumententests?!

Mit diesen Einstellungen …

#======= USER CONFIGURATION =======
RECORD_TIME_IN_MS = 1000
SAMPLE_RATE_IN_HZ = 4050

[...]

#======= Analyzer Settings =======
BINS = 100
START_AT_HZ = 0
NUMBER_OF_BINS = 10

(BINS = 100 bedeutet hier 100 Hz / bin)

… und eine Geige bei der ich testweise leere Seiten gespielt habe:

G-Saite: ~196 Hz
D-Saite: ~296 Hz
A-Saite: ~440 Hz
E-Saite: ~660 Hz

sind die Ergebnisse der FFT nicht eindeutig,

1 starting...
fft finished
result:          [121.3356, 1.644317, 1.482799, 1.931118, 1.526143, 1.565789, 1.610599, 1.547121, 1.486489, 2.058093]
--- 2580 milliseconds ---
#1 ... done! -- 16384 sample bytes

#2 starting...
fft finished
result:          [120.0026, 4.425074, 7.033318, 4.025768, 2.825592, 2.937139, 3.404047, 4.38974, 5.361692, 3.254139]
--- 2762 milliseconds ---
#2 ... done! -- 16384 sample bytes

#3 starting...
fft finished
result:          [95.1308, 9.295344, 4.569943, 23.60806, 5.714966, 7.270836, 19.90534, 4.020807, 8.542375, 2.737609]
--- 2754 milliseconds ---
#3 ... done! -- 16384 sample bytes

#4 starting...
fft finished
result:          [94.23492, 9.062053, 3.809842, 16.20281, 10.27722, 10.11319, 18.16893, 3.550571, 13.22455, 3.924644]
--- 2675 milliseconds ---
#4 ... done! -- 16384 sample bytes

#5 starting...
fft finished
result:          [99.17566, 10.2003, 16.68968, 10.00826, 6.825119, 5.8455, 9.430215, 2.75995, 19.29402, 9.209433]
--- 2867 milliseconds ---
#5 ... done! -- 16384 sample bytes

Denke aber auch, dass eine Geige mit ihren Obertönen nicht so dolle für Tests geeignet ist wie ein Sinuston.

Spectrograms: Instruments and Timbre

Hier noch eine Aufnahme von mir, leere E-Saite auf der Geige:

… komisch sind die da auch die Klick- / Klopf-Geräusche, die ich ab und an bei den Aufnahmen habe, manchmal aber nicht, die sieht man auch recht gut im Spectrogramm oben.

Hier noch die Daten von @cedric.cfk mit einer Triangel:

result:          [91.2915, 7.234389, 10.98247, 37.4546, 3.174848, 3.147414, 7.297245, 33.58657, 5.962651, 4.893304]
result:          [85.86555, 4.986248, 4.165797, 37.35706, 4.40482, 2.914859, 4.362085, 32.56624, 3.58399, 3.52654]

[clemens]

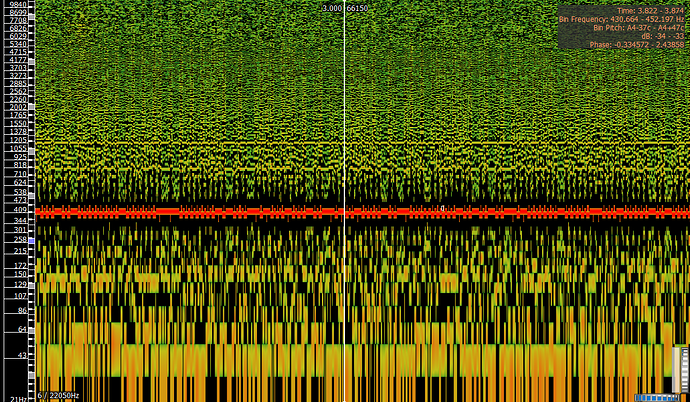
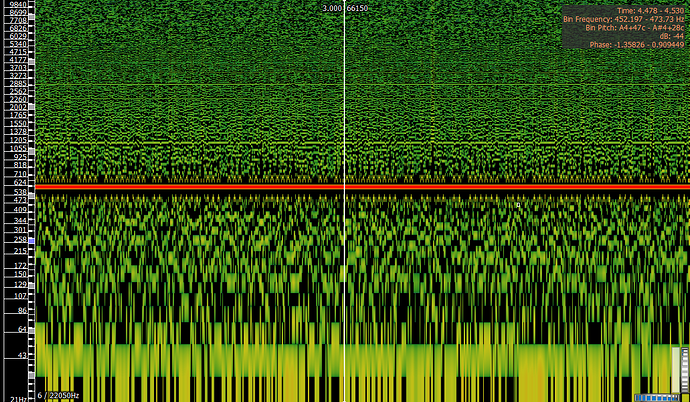
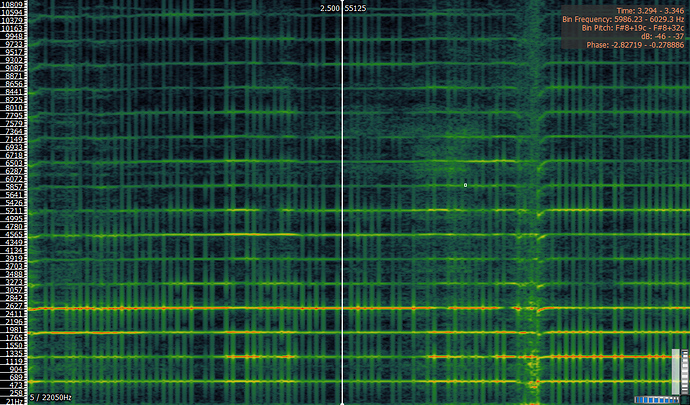
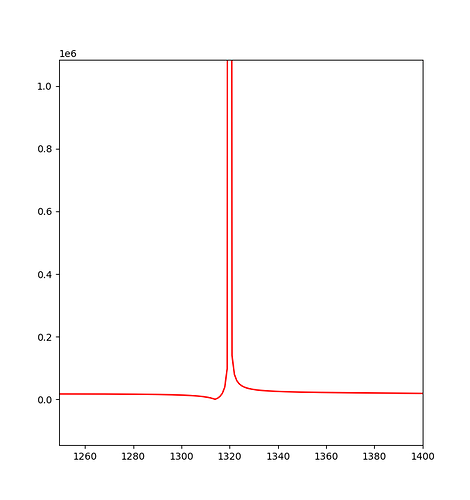
Test mit mehr und kleineren bins

600 Hz

Nun habe ich es nochmal mit mehr (100 Stück) und kleineren bins (je 10 Hz) versucht:

#======= Analyzer Settings =======
BINS = 10
START_AT_HZ = 0
NUMBER_OF_BINS = 100

Ein 600 Hz Ton, erzeugt von https://onlinetonegenerator.com/, mit dem Rechner abgespielt und vom Mic / FiPy aufgenommen und interpretiert ergibt folgenden output:

#3 starting...
fft finished
result:          [
94.23615, 1.217088, 6.288309, 1.247333, 1.189461, 1.364966, 1.307958, 1.041523, 1.200162, 1.436158, 
1.3536, 1.544497, 3.003738, 1.722957, 1.155196, 73.48564, 1.24558, 2.1271, 1.012908, 1.17306, 
1.276368, 1.1738, 1.151565, 0.9671356, 1.241165, 1.000895, 1.070525, 11.58803, 1.74333, 2.700563, 
3.095615, 1.134107, 3.082449, 1.299784, 1.069209, 1.202095, 1.243612, 1.275426, 1.165227, 1.720958, 
1.106034, 1.448803, 2.509693, 1.555842, 1.158046, 23.05586, 1.298197, 1.558852, 1.231459, 1.172899, 
1.019086, 1.135609, 0.9250917, 1.388259, 1.514728, 1.059006, 1.199727, 21.79502, 1.405007, 2.198762, 
2.799765, 1.30749, 2.01305, 1.089083, 0.943228, 1.035334, 0.9973255, 0.8943855, 1.130496, 3.372697, 
1.184806, 1.905699, 2.934093, 1.546395, 1.29897, 9.935121, 1.016957, 1.085351, 1.330705, 1.123706, 
1.024642, 1.072068, 1.028334, 1.299006, 1.700616, 1.168364, 1.243731, 58.28012, 0.9583488, 1.679045, 
1.699107, 1.200472, 1.021757, 0.9552715, 1.102398, 0.9963362, 0.9079949, 0.925675, 1.063031, 4.810687]
--- 6736 milliseconds ---
#3 ... done! -- 32768 sample bytes

Je Zeile ist der output oben mit 10 bins angeordnet, d.h. 600 Hz wären Ende 6. / Anfang 7. Zeile, da ist in Zeile 6 drittletzte Position ein lokales Maxima von 21,7, was rein rechnerisch 580 Hz wären. Aber auch ein Wert von 9,9 bei 760 Hz und 58 bei 880 Hz?? Any idea? Obertöne können es ja nicht sein. Der erste Oberton von 600 Hz wäre die doppelte Frequenz, d.h. 1200 Hz.

Nochmal eine zweite Messung eines 600 Hz-Tons, mit einem anderen Ton-Generator, nämlich Online Tone Generator - generate pure tones of any frequency , Einstellung: Sinuston erzeugt:

[
95.60584, 0.9878141, 10.16923, 1.264853, 1.291657, 0.9595061, 1.069458, 1.733402, 0.8814992, 2.116048, 
0.9408666, 1.156405, 1.261833, 2.508319, 1.529246, 34.95011, 1.10587, 2.467984, 1.197672, 0.9816369, 
6.521753, 0.8908521, 4.858572, 1.334469, 1.183169, 1.989548, 1.164346, 4.582137, 0.9791201, 1.098134, 
1.072338, 1.084168, 9.031716, 0.9604693, 1.728114, 1.70322, 1.295593, 1.721711, 0.9422603, 3.701298,
1.048197, 1.115345, 1.024298, 1.773967, 1.521037, 19.99919, 0.9650134, 1.1809, 1.469502, 1.139276, 
7.744112, 0.9303907, 7.39395, 1.131552, 1.996215, 1.356349, 1.383206, 20.22702, 1.208358, 1.162885, 
1.464888, 1.11718, 4.464071, 0.9310115, 1.759554, 0.9971821, 1.028176, 1.730568, 1.395603, 8.157974, 
1.035325, 1.055992, 1.161947, 1.268519, 1.252383, 8.173367, 0.9125403, 2.299614, 1.048447, 0.8687067, 
4.129266, 0.8356557, 4.483834, 0.9610747, 1.497299, 3.099997, 0.9852068, 39.10541, 0.8204429, 1.918125, 
1.014926, 1.050969, 3.13162, 1.018916, 1.057986, 0.9591295, 0.9381236, 1.526564, 1.187854, 6.845119
]

Maxima von 34 bei 160 Hz, 19 bei 460 Hz, 20 bei 580 Hz, 39 bei 880 Hz???

Und eine Messung mit der Einstellung Rechtecktonkurzve statt Sinuston

[
95.534, 0.9970008, 11.81684, 0.990441, 2.828693, 1.102834, 0.9377657, 4.02583, 1.137756, 5.617577, 
1.158688, 1.441499, 1.023527, 1.878172, 0.903055, 27.66915, 1.16545, 2.664362, 1.233621, 1.166498, 
5.668086, 0.9482989, 3.914526, 1.027133, 1.072372, 2.534729, 1.087083, 15.50659, 1.01908, 2.052005, 
1.532536, 1.107977, 8.976285, 0.7882874, 3.132228, 0.8852935, 0.8883502, 3.620005, 1.208108, 6.900745, 
1.101622, 1.036637, 0.7894821, 2.020242, 0.862628, 10.75814, 0.8365181, 2.091101, 1.197328, 1.305463, 
4.271015, 0.8487687, 4.362002, 1.168851, 1.043518, 2.296273, 0.9237085, 13.67776, 0.8878838, 1.548308, 
1.711679, 1.119342, 6.251703, 1.123245, 2.644144, 1.272126, 1.664974, 2.126316, 0.8491895, 7.583457, 
0.8417312, 1.215318, 0.7551151, 1.363465, 0.9173303, 13.85745, 0.9225768, 2.370693, 1.006334, 1.225731, 
3.308033, 0.7792674, 4.259442, 1.044005, 1.233935, 1.333618, 1.100028, 37.9897, 1.097137, 1.677824, 
1.210835, 1.083182, 5.169371, 0.8803646, 2.466893, 0.9983652, 0.9670907, 2.166277, 1.103819, 8.025347
]

Etwas verändert Werte, aber immer noch Maxima bei 160, 460 , 580, 760 (neu), 880 Hz!

Kontrollmessung 0 Hz

Hier noch die Kontrollmessung ohne irgendeinen Ton abzuspielen:

[
101.7939, 15.53647, 5.422969, 4.409819, 2.797036, 3.318894, 2.875359, 3.421741, 2.123188, 2.145386, 
2.608374, 2.177628, 1.686815, 2.006869, 2.679739, 1.939326, 2.250866, 2.19083, 1.886185, 1.853829, 
1.986694, 1.69255, 1.631477, 1.945275, 1.938631, 1.861386, 2.67258, 2.046509, 2.06057, 2.210608, 
1.715767, 1.769471, 1.855928, 1.657757, 1.832286, 2.363966, 1.522035, 2.235336, 1.909964, 2.00074, 
1.659853, 1.952993, 1.968097, 1.621241, 1.82188, 2.129631, 1.649235, 1.669234, 1.500869, 2.039399, 
2.185206, 1.590029, 1.768338, 2.056099, 2.045014, 1.741056, 1.506912, 1.68753, 1.961407, 1.506467, 
1.542596, 1.913048, 1.710063, 1.837583, 1.415657, 1.708787, 1.830134, 1.999236, 1.509389, 1.573184, 
1.563322, 1.583483, 1.677824, 1.656365, 1.341785, 1.845791, 1.591146, 1.665387, 1.552775, 1.371013, 
1.342636, 1.732217, 1.384431, 1.467128, 1.662403, 1.373346, 1.680919, 1.858915, 1.62084, 1.593713, 
1.677161, 1.834036, 1.864152, 1.554897, 2.869913, 2.587478, 2.295326, 2.045395, 2.948433, 2.692298
]

Auch hier wieder der sehr hohe Wert des ersten bins!!

Interpretation bin 0

Zum hohen Wert unseres ersten bins habe ich noch etwas bei Adafruit gefunden:

Finally, the output of the FFT on real data has a few interesting properties:

• The very first bin (bin zero) of the FFT output represents the average power of the signal. Be careful not to try interpreting this bin as an actual frequency value!
• Only the first half of the output bins represent usable frequency values. This means the range of the output frequencies detected by the FFT is half of the sample rate. Don’t try to interpret bins beyond the first half in the FFT output as they won’t represent real frequency values!

Ich weiß nicht, ob das nur auf unsere FFT zutrifft oder nur unsere und die bei Adafruit verwendete Implementierung, an vielen anderen Stellen im Netz werdern alle bins interpretiert und auch das erste bin “ganz normal” verwendet. Ggf. filter ander Impelmentaionen das schon vorweg raus? @cedric.cfk könntest du dir das nochmal anschauen was hier bei uns genau passiert und ob das von Adafruit beschriebene bei unseren Daten auch auftritt und wir das erste bin (“bin zero” steht bei Adafruit) nicht interpretieren dürfen?

[MKO]

Ich geh mal davon aus, dass für unser bin0 das gleiche wie bei Adafruit gilt, die verwenden soweit ich weiß ebenfals das Ulab Modul auf Cpython.

[poesel]

Ich habe ehrlich gesagt gar keine Ahnung von dem Thema - es interessiert mich aber.
Auch ein bisschen rumprobiert - allerdings nicht mit ulab sondern mit scipy. Ich hab mir von Sine Tone Generator einen 440Hz Ton kopiert und dann damit bearbeitet:

import matplotlib.pyplot as plt
from scipy.fftpack import fft
from scipy.io import wavfile # get the api
fs, data = wavfile.read('audiocheck.net_sin_440Hz_-3dBFS_3s.wav') # load the data
a = data.T.tolist() # this is a two channel soundtrack, I get the first track
b=[(ele/2**8.)*2-1 for ele in a] # this is 8-bit track, b is now normalized on [-1,1)
c = fft(b) # calculate fourier transform (complex numbers list)
d = round(len(c)/2)  # you only need half of the fft list (real signal symmetry)
plt.plot(abs(c[:(d-1)]),'r') 
plt.show()

Den Code habe ich wiederum von Stackoverflow (etwas modifiziert, da waren zwei bugs drin).
Interessanterweise kommt da ein peak bei 1320Hz raus - also 3x Frequenz des Tons.

Hmmm

Btw in dem Kommentar steht aber auch, das man nur die Hälfte des Ergebnis braucht (wegen Symmetrie).

[cedric.cfk]

Im Internet habe ich leider nichts dazu gefunden wie die fft Rückgabe von ulab interpretiert werden soll.

Daraufhin habe ich einen einfachen Test ausgeführt:

>>> fft.spectrogram(np.array([1,2,3,4,5,6,7,8]))
array([36.0, 10.4525, 5.656854, 4.329568, 4.0, 4.329569, 5.656855, 10.45251], dtype=float)

Hier sieht man, dass das erste Element alleine steht und die restlichen Elemente Symmetrisch sind.

Somit gehe ich davon aus, dass @clemens Vermutung zutrifft.
Das oben genannten Programm benutzt bereits nur die erste hälfte der Daten. Allerdings werde ich das erste Element nun gesondert angeben.